Spatial Modelling of Data for the e-Atlas
The interactive maps and KML map files found on the e-Atlas often contain spatially modelled data. These notes explain how the modelling was undertaken.
For each modelled data set, there are typically two maps available:
- the spatially modelled estimated values of the response variable, and
- the spatial precision of those estimates.
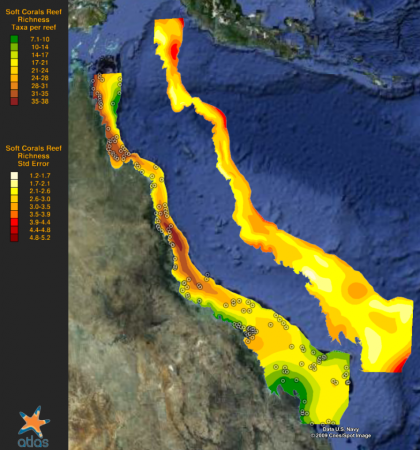
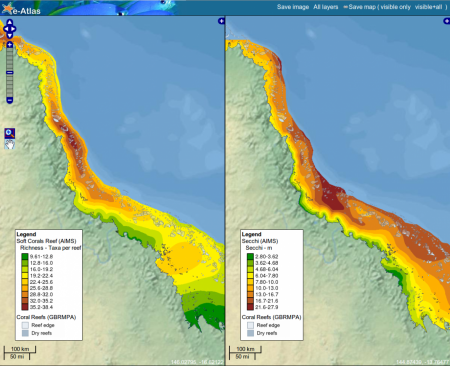
For the KML format, the raw data are additionally included for each site and can be compared to the estimated values of the map. The estimated response and precision are mapped use 9-colour bands that aid interpretation of the estimated values and their precision. Examples of these maps are shown in Figures 1 & 2 below.
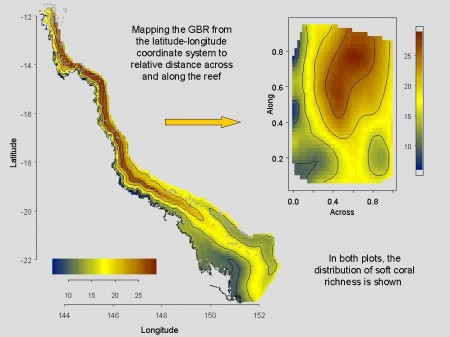
Latitude and longitude are normally used for the spatial component of such models. However, the Great Barrier Reef (GBR) runs from ~ SE to NW and has physical and ecological gradients which run typically across and (to a lesser degree) along the shelf, are therefore tilted 45° to the geodesic system. To improve the analysis and graphical representation of the spatial patterns, the latitude/longitude data were converted into relative distance across and along the Great Barrier Reef (Fig. 3). Relative distance across the Great Barrier Reef (henceforth: “across”) is defined as the distance of a site to the coast, divided by the sum of distances to the coast and to the outer edge. Relative distance along the GBR (henceforth: “along”) is similarly defined as the distance to the northern end of the GBR divided by the sum of distances to the northern and southern ends of the GBR. This has the effect of mapping the Great Barrier Reef Marine Park (GBRMP) to a rectangle or unit square, if we assume that units across equate to units along (Fig. 3). The coordinates of the across-along system are locally orthogonal, and run at right angles and parallel to the coast, taking advantage of the fact that many processes are affected by the natural geometry of the GBR. Such presentation gives better resolution in particular of the steep gradients across the narrow shelf of the northern GBR (De'ath et al 2009, Fabricius & De'ath 2008).
A local regression spatial smoother was used to model richness, and the fitted surface was then mapped back to latitude-longitude coordinates. The maps were generated from the values predicted from statistical models for each data set, by fitting smooth, 2‑dimensional surfaces over the area of the GBR. Specifically, generalised additive models (Wood 2006) were used to analyse the spatial variation across and along the continental shelf over the entire GBR. These models incorporate smoothers to estimate the relationships between the response and predictor variables, and as such can account for non-linearity. Spline smoothers, which are interpolating methods for fitting smooth curves to data, were used. The smooth 2D spatial surfaces were estimated with thin plate splines (Wood 2003), which estimate a smooth function of multiple variables. The smoothness of the fit (i.e. how straight or wobbly the relationship) was determined by fitting a series of models with a fixed range of degrees of freedom, and selecting the smoothness that minimised the prediction error (PE). The PE of a model is defined as the sum of squared prediction errors (observed - predicted values) divided by the sum of squared observations about the overall mean. An upper maximum degrees of freedom of 25% of the sample size was used to prevent overfitting. As stated above, generalised additive models were used. These models are 'generalised' in the sense that they allow for residual variation to be non-normally distributed, and for predictions of the response variable to be constrained within a specified range (e.g. fish counts cannot be negative). For the models used in this report, link and variance functions were selected according to the type of response variables used for each analysis. Response variables measuring proportions (or percentages) were modelled with a logit link and binomial variance function. Abundances variables were typically modelled with a log link and Poisson variance function, and all other variables were modelled with a constant link and normal variance function.
References
De'ath G, Fabricius K and Lough J. 2009. Declining Coral Calcification on the Great Barrier Reef, Science 323:116–119.
Fabricius K and De'ath G. 2008. photosynthetic symbionts and energy supply determine octocoral biodiversity in coral reefs. Ecology 89(11):3163–3173
Wood SN 2003. Thin plate regression splines. Journal of the Royal Statistical Society, B. 675: 95-114.
Wood SN 2006. Generalized additive models: an introduction with R. Chapman and Hall/CRC, Boca Raton.